英国数学家、牛津大学教授安德鲁·怀尔斯被授予2016年阿贝尔奖。3月15日,挪威科学与文学院宣布,安德鲁·怀尔斯因其为证明费马大定理方面做出的杰出贡献而摘夺今年的阿贝尔奖。
阿贝尔奖是挪威设立的数学界大奖。2002年,为纪念挪威著名数学家尼尔斯·亨利克·阿贝尔(N.H.Abel,1802-1829)200周年诞辰,挪威政府宣布将开始颁发此奖,意在弥补诺贝尔科学奖项中没有数学奖的遗憾。自2003年起,由挪威自然科学与文学院的五名数学家院士组成的委员会负责宣布获奖人,授予每年评选出的最杰出的数学家奖金600万挪威克朗(约合450万人民币)。如今,阿贝尔奖已经成为数学学科中最有声望的国际性奖项。2015年阿贝尔奖的得主是著名数学家约翰·纳什,而他也正是在领奖回国后返家的路上因车祸去世的。
安德鲁·怀尔斯
挪威科学与文学院在颁奖词中声明:怀尔斯通过证明半稳定椭圆曲线是模曲线,出色地证明了费马大定理,从而在数论领域开创了一个新时代。
得知获奖后,怀尔斯对前来采访的媒体表示自己感到非常荣幸,不过还没想好怎么使用这600万克朗。
费马大定理由法国数学家费马提出,该定理断言当整数n >2时,关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。费马没有写下证明,而他的其它猜想对数学贡献良多,由此激发了许多数学家对这一猜想的兴趣,是数学史上著名的谜题之一。费马提出这一定理后,历经300多年历史无人证实,直到1995年怀尔斯将证明过程刊发在《数学年刊》(Annals of Mathematics)上。
怀尔斯于1953年生于英国剑桥,在牛津大学获学士学位,随后在剑桥大学获得博士学位。他的主要职业生涯是在英国牛津大学和美国普林斯顿大学度过的。
怀尔斯在接受《卫报》采访时回忆,他10岁时就迷上了这个问题。“当我第一次看到费马大定理时,我就被吸引住了,当时才10岁的我并不知道这是个著名的数学猜想,整个十几岁的年纪我都在尝试解答这一问题。我记得我刚上大学时得出了第一个证明过程,但后来发现是错误的。”
1993年,在普林斯顿大学从事7年研究后,怀尔斯宣称证明了费马大定理,并于剑桥大学举行讲座向200多名研究人员推演过程。证明过程获得了同行的肯定,引发轰动。但同年年末,一位数学家在检查怀尔斯的证明过程时发现了一个错误。
怀尔斯力求弥补这个证明漏洞,之后一年时间里,在他之前的博士研究生理查德·泰勒(Richard Taylor)的协助下补上了这个漏洞。1996年怀尔斯将修正后的证明过程刊登在《数学年刊》上,获得了业内数学家的首肯。怀尔斯也因此获得了1998年国际数学联盟的特别荣誉,一个特殊制作的菲尔兹奖银质奖章。
当被询问到解决了一个古老谜题后是什么感受?怀尔斯说:“令人兴奋,就好像我们在生活中一直模糊不清,看不清未来感到沮丧时,忽然你拥有了看清一切的洞察力。”
达到这一职业高峰也让怀尔斯暂时有些迷茫,“很难立刻回到正常的工作继续下一个挑战,但我相信一段时间后,数学的美会重新让我沉迷其中。”
摘自: http://www.thepaper.cn/newsDetail_forward_1444693_1
费马大定理,又被称为“费马最后的定理”,由法国数学家费马提出。
它断言当整数n >2时,关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。
被提出后,经历多人猜想辩证,历经三百多年的历史,最终在1995年被英国数学家安德鲁·怀尔斯证明。
德国佛尔夫斯克宣布以10万马克作为奖金奖给在他逝世后一百年内,第一个证明该定理的人,吸引了不少人尝试并递交他们的“证明”。在一战之后,马克大幅贬值,该定理的魅力也大大地下降。
猜想提出
费马在阅读丢番图(Diophatus)《算术》拉丁文译本时,曾在第11卷第8命题旁写道:“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证法 ,可惜这里空白的地方太小,写不下。”
(拉丁文原文: "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.")
毕竟费马没有写下证明,而他的其它猜想对数学贡献良多,由此激发了许多数学家对这一猜想的兴趣。数学家们的有关工作丰富了数论的内容,推动了数论的发展。
对很多不同的n,费马定理早被证明了。其中欧拉证明了n=3的情形,用的是唯一因子分解定理;费马自己证明了n=4的情形。
1825年,狄利克雷和勒让德证明了n=5的情形,用的是欧拉所用方法的延伸,但避开了唯一因子分解定理。
1839年,法国数学家拉梅证明了n=7的情形,他的证明使用了跟7本身结合得很紧密的巧妙工具,只是难以推广到n=11的情形;于是,他又在1847年提出了“分圆整数”法来证明,但没有成功。
1844年,库默尔提出了“理想数”概念,他证明了:对于所有小于100的素指数n,费马大定理成立,此一研究告一阶段。但对一般情况,在猜想提出的头二百年内数学家们仍对费马大定理一筹莫展。
1955年,日本数学家谷山丰首先猜测椭圆曲线与另一类数学家们了解更多的曲线——模曲线之间存在着某种联系;谷山的猜测后经韦依和志村五郎进一步精确化而形成了所谓“谷山—志村猜想”,这个猜想说明了:有理数域上的椭圆曲线都是模曲线。这个很抽象的猜想使一些学者搞不明白,但它又使“费马大定理”的证明向前迈进了一步。
1985年,德国数学家弗雷指出了谷山——志村猜想”和费马大定理之间的关系。他提出了一个命题:假定“费马大定理”不成立,即存在一组非零整数:
a,b,c
使得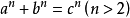
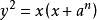 乘以
乘以
的椭圆曲线,不可能是模曲线。
尽管他努力了,但他的命题和“谷山——志村猜想”矛盾,如果能同时证明这两个命题,根据反证法就可以知道“费马大定理”不成立,这一假定是错误的,从而就证明了“费马大定理”。但当时他没有严格证明他的命题。
1986年,美国数学家里贝特证明了弗雷命题,于是希望便集中于“谷山——志村猜想”。
1993年6月,英国数学家安德鲁·怀尔斯宣称证明:对有理数域上的一大类椭圆曲线,“谷山—志村猜想”成立。由于他在报告中表明了弗雷曲线恰好属于他所说的这一大类椭圆曲线,也就表明了他最终证明了“费马大定理”;但专家对他的证明审察发现有漏洞。怀尔斯不得不努力修复着一个看似简单的漏洞。
怀尔斯和他以前的博士研究生理查德·泰勒用了近一年的时间,用之前一个怀尔斯曾经抛弃过的方法修补了这个漏洞,这部份的证明与岩泽理论有关。这就证明了谷山-志村猜想,从而最终证明了费马大定理。他们的证明刊在1995年的《数学年刊》(Annals of Mathematics)之上。
怀尔斯因此获得1998年国际数学家大会的特别荣誉,一个特殊制作的菲尔兹奖银质奖章。
摘自:http://baike.baidu.com/link?url=qbTyXP6vf4iCF7uAPZKVmRu4jMnExeXGsAzgjHX7jyC7CcXKhhOWd22G-w9qqgp-jtey917BM66M96arQJNr9gjqTZM8ewYmQ16dM5YIHTa