谈弧度，就必须先谈下角度，如果世界上只有弧度，没有角度，我相信大家也就不会疑惑为什么会有弧度制了。
1.1 角度为什么出现？
角度的出现，是源于对圆周运动的观察。
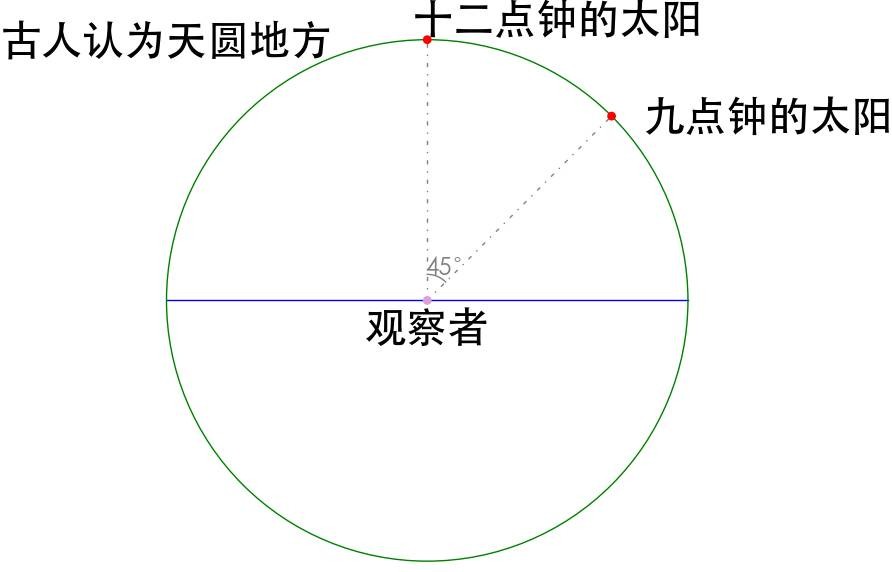
这个世界上最大最显眼的圆周运动就是太阳，就算我们现代人知道地心说是错误的，可是以我们的尺度来说，抬头还是观察到太阳在做圆周运动。
作为观察者，我们也非常自然的，以我们为中心，开始计算太阳相对我们的移动，这就开始出现了角度。
1.2 圆周为什么是360°？
地球围绕太阳公转，而遥远的十二星座仿佛固定在圆柱形天幕上:
地球上的我们就像看走马灯一样，随着地球的公转，在特定的时间看到特定的星座。古人发现了这个规律，并且以星座为参照物，近似观察出循环周期为360天，也就是一年。
因此，天就被等分成了360份，也就是圆被等分成了360份。虽然后来古人慢慢发现了一年实际上是365天，但是因为360度已经成为习惯，并且非常好计算，所以就被保留了下来。
1.3 度数是圆周的占比
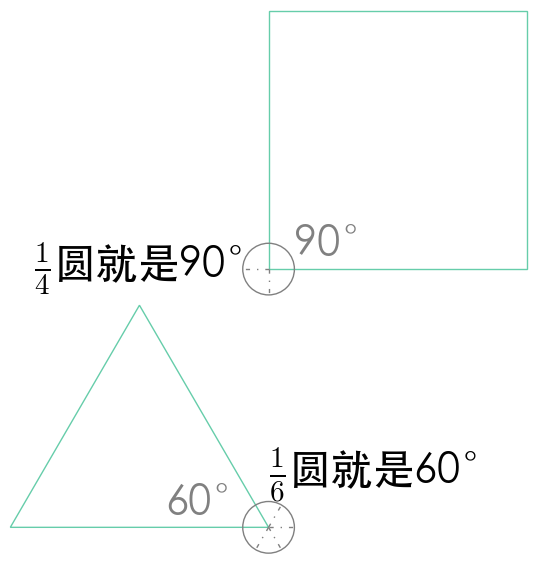
角度似乎已经足够描述圆周运动了，为什么要出现弧度？是来给世界添乱的吗？
2.1 弧度为什么出现？
弧度的出现，刚开始不过是个数学游戏。弧度＝弧长/半径，对于相同的角度这个比值保持不变，所以可以看作角度的另一种表现形式。(其实“弦长/半径”也是定值，为啥不选这个作为弧度呢？可以想想。)
2.2 弧度有什么现实意义？
弧度是从圆周运动进行者的角度来看待圆周运动。
之前说过，古人的世界观是天圆地方，人们的旅行都被视为直线运动。欧式几何里面的直线笔直的延伸到无穷远处。
可是，事实是，地球是圆的，随着技术的发展，大航海时代的来临，大家越来越认识到这一点。传统意义上的直线，在地球表面都不复存在，必须重新定义直线的含义。
弧度也是在这样的环境下开始发扬光大：
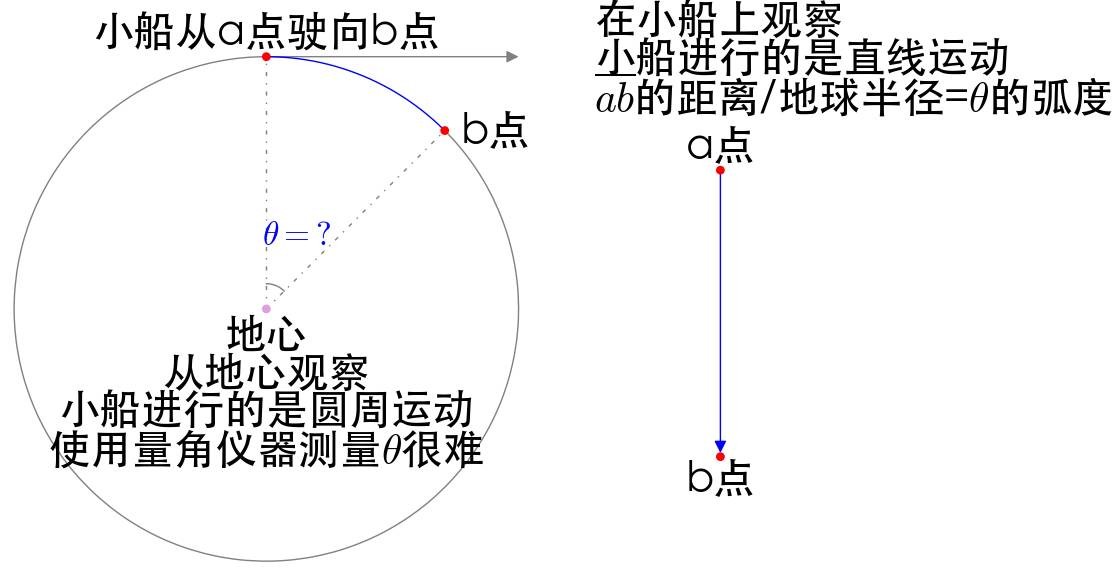
知道了移动的角度，也就知道了经纬度，就可以通过地图进行导航，而利用弧度，大大简化了这一过程。
“海里”这个航海单位也是弧度在大航海时代的产物。
2.3 弧度可以把圆周运动转为直线运动
这种转换有了之后，就可以很方便的测量汽车的直线速度了。汽车在车胎附近安装一个传感器，测出车胎的转速（比如10弧度/秒），乘以半径（比如1米），就得到了汽车的直线速度（这里就是10米/秒)。有的出租车换了更小直径的轮胎而不修改行车电脑里面的轮胎半径，就可以轻松的“偷里程”。所以，学习多么的重要啊！
2.4 弧度帮助理解重要极限
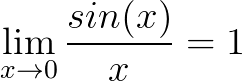，这是个很重要的极限，考试也会经常用到，但是他的几何意义是什么呢？
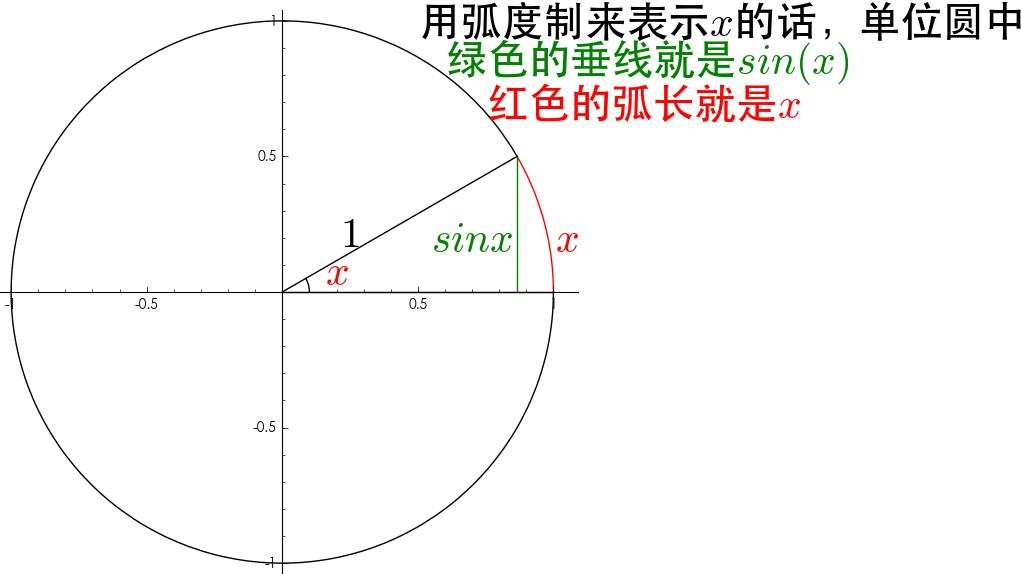
2.5 在现代数学中，弧度是最基本的概念
弧度使得角度和实数统一在了一起。对于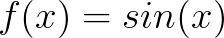 
这个函数而言，如果 使用角度，就很难去理解这个方程，一边的单位是度，一边是无单位的实数。而使用弧度可以很好的解决这一问题，使得 和 都是无单位的数。
弧度开启了三角函数的大门。欧拉在他的著作《无穷小分析概论》就提出了弧度，并且作出了三角函数线（这也是非常有趣的概念，在这里就不展开了），通过弧度和三角函数线，第一次定义了三角函数！这也是欧拉在数学上的重大贡献之一。此时，三角分析才开始和函数这个有力的工具挂上钩。
- 角度是对圆周运动的观察，弧度是对圆周运动的进行
- 角度是有单位的，弧度是无单位的，所有三角函数都应使用弧度
个人觉得，在现代教育中，弧度制应该尽早的引入，而去弱化角度制，让学生尽早形成对弧度制的直觉认知。就好比加减乘除虽然重要，但是在微积分才是现代数学的基础。
